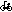or 
で極限まで迷ったけど､
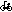で正解だった
てか､医学部って大変そう
受験
に面接とかあるし
...いや､そも
血を見るコト自体が大のニガテ
な俺には､
その時点で、かなり無縁な学部なんだけどね
w
昨日の問題...
《ア》は､
『△ABCにおいて､
AB↑・AC↑=(AB^2+AC^2-BC^2)/2
が成り立つ｡』を用いる｡
これは､ガチで美味しい
《イ》《ウ》は､
35^2-29^2
=(35+29)(35-29)
=64・6
に変形して計算
これもかなり美味しい
《エ》《オ》は､おまけ
《ア》を使うと､今年のセンター数学Ⅱ･B【4】の最初は瞬殺
『四面体OABCにおいて､
OA=OB=BC=√2
OC=CA=AB=√3である｡
このとき､
OA↑･OB↑
OB↑･OC↑
OC↑･OA↑
をそれぞれ求めよ｡』
(※問題を抜粋し､表記を変更｡)
かなり役立つでしょう...
PR
今日は､後期になって､初めての授業
とかもあったし､
それなりに新鮮
な日だった
...有名な裏(?)技
(自分も知らなかったけどねｗ)
△ABCは､
AB=5
BC=4
AB↑・AC↑=29
を満たしている｡
このとき､AC=《ア》である｡
よって､△ABCの面積をSとすると､
S=《イ》√《ウ》である。
したがって､△ABCに内接する円の半径をrとすると､
r=√《エ》/《オ》である｡
問題も､今年のセンターに出てもよさそうな感じかもね
今日は駿台の模試
...本当に笑えない結果
化学20~25
物理15~20
100点満点なのに...(－Ａ－;)
という訳で､
10月は『理科の月』だ
といいたい所だけど､
国数英も
割くらいだし...
本当に鬱だ orz ←
非常に不安だ
ちなみにn=1代入ね
...本当に笑えない結果
化学20~25
物理15~20
100点満点なのに...(－Ａ－;)
という訳で､
10月は『理科の月』だ
といいたい所だけど､
国数英も
割くらいだし...本当に鬱だ orz ←
非常に不安だ
ちなみにn=1代入ね
数列{a[n]}は､
全ての自然数nに対して
Σ[k=1,n]a[k]=－9n(n+1)
を満たしている。このとき
a[n]=《アイウ》n である｡
誰も見てないのに､一人で『裏技
』とか悲しすぎるんで ←誰かが解いたら､載せようかな
明日から後期か...
今日は､いろいろあって､
宮崎名物(?)の『チキン南蛮』
を晩飯に作った
(難しくなかったけどね｡)
てか､
35時間とか､全然だった
明日からは...
